| 들어가며
연속확률 분포중 카이제곱 분포에 대해 이해해보자
| 개념정리
카이제곱 분포는 데이터의 분산이 퍼져있는 모습을 분포로 만든 것이다.
데이터를 파악할때 중심 위치(평균)와 퍼짐 정도(분산)이 중요한데 카이제곱은 바로 분산의 제곱값에 대한 분포다.
독립변수가 명목치인 어떤 표본이 모집단의 분포와 같은지 다른지 검정할때 활용된다.
카이제곱 분포는 분산의 제곱된 값을 보여주기 때문에 마이너스(-) 값으로 나오지 않고 (+) 값만 존재하며 좌우 비대칭의 분포를 따른다.
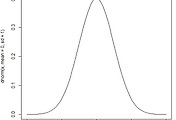
| 카이제곱 분포 그래프
library(ggplot2)
ggplot(data.frame(x=c(0,10)), aes(x=x)) +
stat_function(fun=dchisq, args=list(df=1), colour="black", size=1) +
geom_text(x=0.6, y=1, label="df=1") +
stat_function(fun=dchisq, args=list(df=2), colour="blue", size=1) +
geom_text(x=0, y=0.55, label="df=2") +
stat_function(fun=dchisq, args=list(df=3), colour="red", size=1) +
geom_text(x=0.5, y=0.15, label="df=3") +
stat_function(fun=dchisq, args=list(df=5), colour="green", size=1) +
geom_text(x=1.5, y=0.05, label="df=5") +
ggtitle("Chisq-Distribution")
그래프를 df값 즉 자유도에 따라서 그래프 모양이 달라지는 것을 알 수 있다.
자유도3을 기준으로 보면 초반에는 가파르게 오르다가 우측으로 갈 수록 내려가는 형태다.
자유도는 쉽게말해 변수의 수(n-1)라고 보면 된다.
보다 정확한 정의는 다음 링크를 참고 바란다.
▶통계용어 - 자유도(degrees of freedom)
만약 평균이 0이고 표준편차가 1인 표준 정규분포에서 3개의 데이터를 관측해 이에 대한 카이제곱 분포를 보고자 한다면
df=3의 그래프 형태를 보인다.
| R에서의 카이제곱 분포 함수
구분 | R 함수 |
확률 밀도 함수 (Density function) | dchisq(x, df, ncp=0, log=FALSE) |
누적 분포 함수 (Cumulative distribution function) | pchisq(q, df, ncp=0, lower.tail =TRUE, log.p=FALSE) |
분위수 (Quantile) | qchisq(p, df, ncp=0, lower.tail=TRUE, log.p=FALSE) |
난수 (random) | rchisq(n, ncp=0) |
카이제곱 분포는 직접 확률을 구할 때 사용하는 분포가 아니라, 신뢰 구간과 가설검정, 독립성 검정등에 사용한다.
다음의 예를 보자
류머티스 관절염 환자에 대한 신약 테스트 결과를 모아 놓은 Arthritis 데이터 프레임을 활용한다.
이 데이터는 실제 신약을 투약한 사람과 위약(가짜약, 환자에게 진짜 약이라 믿도록 플라시보 효과만을 준다)을 놓고 개선여부를 기록한 데이터이다.
[참고 소스 출처 : http://rfriend.tistory.com/112]
> install.packages("vcd")
> library(vcd)
> str(Arthritis)
'data.frame': 84 obs. of 5 variables:
$ ID : int 57 46 77 17 36 23 75 39 33 55 ...
$ Treatment: Factor w/ 2 levels "Placebo","Treated": 2 2 2 2 2 2 2 2 2 2 ...
$ Sex : Factor w/ 2 levels "Female","Male": 2 2 2 2 2 2 2 2 2 2 ...
$ Age : int 27 29 30 32 46 58 59 59 63 63 ...
$ Improved : Ord.factor w/ 3 levels "None"<"Some"<..: 2 1 1 3 3 3 1 3 1 1 ...
> View(Arthritis)
#####
Treatment는 치료여부로 Treated가 실제 투약, Placebo가 가짜약 투약이다.
Improved는 개선여부로 Some, Marked, None로 효과가 기록되어 있다.
ID : patient ID.
Treatment : factor indicating treatment (Placebo, Treated).
Sex : factor indicating sex (Female, Male).
Age : age of patient.
Improved : ordered factor indicating treatment outcome (None, Some, Marked).
이제 이 데이터를 카이제곱 검정을 해보자
> #install.packages("gmodels")
> library(gmodels)
> CrossTable(Arthritis$Treatment, Arthritis$Improved,
expected = TRUE,
chisq = TRUE) # chisq-test
Cell Contents
|-------------------------|
| N |
| Expected N |
| Chi-square contribution |
| N / Row Total |
| N / Col Total |
| N / Table Total |
|-------------------------|
Total Observations in Table: 84
| Arthritis$Improved
Arthritis$Treatment | None | Some | Marked | Row Total |
--------------------|-----------|-----------|-----------|-----------|
Placebo | 29 | 7 | 7 | 43 |
| 21.500 | 7.167 | 14.333 | |
| 2.616 | 0.004 | 3.752 | |
| 0.674 | 0.163 | 0.163 | 0.512 |
| 0.690 | 0.500 | 0.250 | |
| 0.345 | 0.083 | 0.083 | |
--------------------|-----------|-----------|-----------|-----------|
Treated | 13 | 7 | 21 | 41 |
| 20.500 | 6.833 | 13.667 | |
| 2.744 | 0.004 | 3.935 | |
| 0.317 | 0.171 | 0.512 | 0.488 |
| 0.310 | 0.500 | 0.750 | |
| 0.155 | 0.083 | 0.250 | |
--------------------|-----------|-----------|-----------|-----------|
Column Total | 42 | 14 | 28 | 84 |
| 0.500 | 0.167 | 0.333 | |
--------------------|-----------|-----------|-----------|-----------|
Statistics for All Table Factors
Pearson's Chi-squared test
------------------------------------------------------------
Chi^2 = 13.05502 d.f. = 2 p = 0.001462643
결과를 보면 제일 하단에 카이제곱 검정의 p vlaue가 0.05보다 낮은 0.001462643 을 나타낸다.
따라서 귀무 가설인 H0의 가정인 두 factor 간에 서로 관련성이 없다를 기각하고
대립가설인 H1 "두 factor 간에 서로 관련성이 있다" 를 채택한다.
즉 약 효과가 있다는 말이다.
사실 카이제곱 검정은 위에 함수 말고 chisq.test() 함수를 활용하는데
여기서는 독립성 검정설명이 목적이 아니기 때문에 다른 포스트에서 다루기로 한다.
| 참고자료
블로그 : http://rfriend.tistory.com/112, http://math7.tistory.com/57
'Data Science > 통계이론' 카테고리의 다른 글
| 정규분포(Nomal distribution) 이해하기 :: Data 쿡북 (0) | 2017.09.05 |
|---|---|
| Bias - Variance Trade-off(편향-분산 트레이드 오프) 이해 그리고 머신러닝 학습 정도 이해 :: Data 쿡북 (2) | 2017.08.21 |
| 아주 잘 정리된 공공데이터 포털 모음 공유 :: Data 쿡북 (0) | 2017.08.20 |
| 각종 통계 정보 및 데이터를 얻을 수 있는 Site 정리 :: Data 쿡북 (0) | 2017.01.07 |
| 그리스 문자 / 표기 정리 :: Data 쿡북 (0) | 2017.01.05 |



댓글