오늘은 주성분 분석에 대한 간략한 소개와 함께 R을 활용해 실습한 내용을 공유할까 한다.
사실 주성분에 대한 내용은 여러 블로깅에 이론적(수학적)으로 잘 소개되어 있기 때문에 여기서는 수학적 배경 보다는 R 활용에 초점을 맞출까 한다.
참고로 이론이나 관련 수학적 지식은 본 블로깅 최 하단 참고자료에 링크를 걸어 둔다.
필자도 많이 참고한 site 이다.
| 배경
주성분 분석은 Person(1901)에 의해 처음 제기되어 Hotelling(1936)에 의해 독자적으로 발전했다.
Hotelling은 변수들 간의 상관 구조를 분석하기 위해, p개인 원래 변수들의 변이(Variation)1을 결정하는데 더 낮은 차원의 서로 독립적 요인을 구하여 이를 주성분이라 부르게 된다.
서로 연관되어 있는 변수들의 정보를 최대한 확보하면서 적은 수의 새로운 변수들(주성분)을 생성하는 방법을 의미하는 것이다.
그래서 왜 쓰는지를 설명하면..
사실 우리가 어떤 한 대상을 설명하고자 할 때 대상을 설명하는 x변수의 개수가 너무 많을 경우 다음과 같은 문제가 생길 수 있다.
- 컴퓨터 처리량이 많아지는 문제
- 너무 복잡한 시각화 문제
- 분석에 그리 영향이 없는 변수가지 포함할 경우 비효율적인 문제
- 데이터에 대한 해석 어려워지는 문제
따라서 분석할 때 변수의 개수가 많다고 모두 활용하는 것이 꼭 좋은 것은 아니다.
오히려 변수간 다중공선성2이 있을 경우 분석 결과에 영향을 줄 수도 있다.
따라서 많은 변수들을 한번에 쓰기 보다는 정보의 손실을 최소화 하고 다른 몇개의 성분으로 달리 표현해 분석한다면 위의 문제들을 피할 수 있다.
변수를 차원이라고 표현한다면 결국 차원축소를 한다는 의미이기도 하다.
| 차원 축소
차원라고 하면 너무 거창하게 들리는데 결국 대상을 설명하는 변수로 이해하면 된다.
예를 들어 한 개인을 설명할 때 사는곳, 이름, 나이, 성별 등을 들어 특징을 말한다면 각각이 이 모두 차원이다.
따라서 주성분 분석도 차원 축소의 한 방법이라 할 수 있다.
차원 축소를 하면 데이터의 일부가 사라질 수 있지만, 실제 주요 정보는 남겨진다.
그리고 변수에는 오차와 잡음이 섞여 있는데 차원 축소를 하면서 공통 정보만 추출할 경우 오히려 오차와 잡음도 사라질 수 있는 장점이 있다.
차원축소를 하는 방법은 주성분분석 외에
- 요인분석(FA)
- 독립성분분석(ICA)
- 다차원 척도법(MD5)
- 비선형 차원 축소법
등이 있는데 이는 다른 블로깅에서 차차 언급하겠다.
| R 기반의 PCA 실습
지금부터는 R기반의 PCA 실습 내용을 설명한다.
데이터는 "HSAUR" 패키지에 있는 heptathlon 으로 1988년 서울 올림픽 육상 여성 7종 경기에 대한 결과이다.
총 8개의 case 의 데이터 이며
hurdles(110m 허들)
highjump(높이뛰기)
shot(포환던지기)
run200m(200m 달리기)
longjump(멀리뛰기)
javelin(창던지기),
run800m(800m 달리기)
전체 score
의 구조로 데이터가 구성되어 있다.
자, HSAUR 패키지를 설치하고 데이터를 살펴보자
> library(HSAUR)
> data(heptathlon)
> head(heptathlon)
#기초 통계량 확인
> summary(heptathlon)
데이터를 보면
hurdles, run200m, run800m은 값이 작을 수록 좋기 때문에 높은 수가 좋은 점수가 되도록 최대값에서 빼준다.
데이터 분석할 때 이같은 사항을 잘 고려해야 한다.
> hep.data.tmp <- heptathlon
> hep.data.tmp$hurdles <- max(hep.data.tmp$hurdles)-hep.data.tmp$hurdles
> hep.data.tmp$run200m <- max(hep.data.tmp$run200m)-hep.data.tmp$run200m
> hep.data.tmp$run800m <- max(hep.data.tmp$run800m)-hep.data.tmp$run800m
#score 데이터 제외처리 : Score 데이터는 주성분 분석에서 제외시킨다.
> hep.data <- hep.data.tmp[,-8]
> hep.data.tmp[,-8]
> var(hep.data)
#대각선은 분산을 의미하고 다른것은 공분산을 의미한다.
#각 변수별 관계를 확인할 수 있다.
주성분 분석을 실행한다.
주성분 분석은 간단히 prcomp 함수를 사용하면 된다.
#주성분 분석 실행
> hep.data.pca <- prcomp(hep.data, scale. =T) #pr은 principal comp 는 component의 약자
> hep.data.pca
#standard deviations: 는 표준편차를 의미하는것으로 각 변수가 얼마나 많은 부분을 차지하고 있는지를 알려준다.
#scale. = T는 수치간 표준화를 지정하는 것으로 각 변수당 단위가 다르기 때문에 표준화가 필요하다.
#참고로 prcomp 가 아닌 stat 패키지의 princomp도 주성분 분석을 할 수 있는데 여기서는 cor=T를 주면 된다.
> summary(hep.data.pca)
#summary를 하면 주성분 분석에 대한 결과 요약 설명이 나온다.
#Standard deviation : 표준편차
#Propertion of Variance : 분산비율, 각 주성분의 차지하는 비율을 말하며 클 수록 영향도가 그만큼 높다는 의미임
#Cumulative Proportion : 분산의 누적 합계
여기서 주성분 개수를 결정하는 기준은
1. 총 변이에 대한 공헌도 :
Cumulative Proportion의 값이 80% 이상인 것 까지를 보통 하는데 이는 통상적인 기준일 뿐이다.
위 예에서는 PC2 까지의 수치가 0.8078인데 나머지 0.1922정도의 정보 손실을 감수하고 쓰겠다고 결정된다면 PC1과 PC2를 사용하면 된다.
2. 개별 고유값의 크기 :
분산값 즉 표준편차(Standard deviation)의 제곱의 수치가 1이상인 경우를 쓴다.
이는 Kaiser의 규칙을 기준으로 활용한다. 참고로 Jolliffe(1986)는 Kaiser의 1 대신 0.7을 제안한바 있다. 1은 너무 타이트 하다는 의미임..
위 경우에서도 PC2 까지가 적당한 것으로 판단된다.
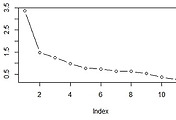
3. 스크리 그림을 통한 판단 :
수평축에 주성분을 놓고 수직축에 해당 주성분에 대응하는 고유값을 연결한 차트임
그래프가 완만해 지는 부분이전 까지만 활용하는 것이 바람직하다는 것이다.
자, 스크리 그림(screeplot)을 그려보자
> screeplot(hep.data.pca, type="lines", pch=1, main="scree plot")
> hep.data.pca$rotation[,1:2]
위 데이터를 보면 PC1의 경우 javelin(창던지기)를 제외한 나머지의 절대값 수치가 높은것으로 볼 때 전반적으로 체력관련 지수를 의미하는 것으로 판단할 수 있다.
PC2는 창 던지기가 가장 큰 것으로 보아 창던지기 지수를 의미한다.
결국 순위권에 들려면 체력과 창던지기를 잘 하는 것이 등수에 영향을 많이 미친다는 것을 알 수 있다.
사람별로 주성분 분석 지표를 보자
> hep.data.pca$x[,1:2] #순위별로 주성분 변수의 값을 알 수 있음
| biplot 으로 주성분 분포를 확인해보자
> biplot(hep.data.pca, main="Biplot")
# 각 개체에 대한 첫 번째, 두 번째 주성분 점수 및 행렬도(biplot)
# 각 개체의 관찰값은 주성분점수로 하고, 각 변수와 주성분과의 관계를 나타내는 주성분 계수를 동시에 나타내어 이들의 관계를 살피려는 다변량 그래프 분석 기법이다.
biplot은 Gabriel(1971)에 의해 제안된 방법으로 다변량 자료가 가지는 정보를 기하적으로 탐색하는 방법이다.
행렬도에서 highjump, run800m, hurdles, longjump가 서로 가까운 곳에 위치하고 javelin은 다른 변수들과 다른 방향에 위치하고 있다.
가까운 거리와 방향일수록 변수들의 상관성이 높아지게 된다.
각 선수 별로 어떤 성향에 가깝게 배치 되어 있는지를 한 눈에 알 수 있다.
[참고자료]
http://blog.naver.com/PostView.nhn?blogId=jindog2929&logNo=10161293384 : 공분산개념
http://rfriend.tistory.com/61 : (5) 차원 축소 - (5-1) 주성분분석 (PCA)
http://rfriend.tistory.com/181 : 고유값 고유벡터
방송통신대학교 다변량분석 강의자료
'Data Science > R 분석과 실습' 카테고리의 다른 글
| F Test(F 검정)의 이해와 R 실습 (3) | 2017.09.27 |
|---|---|
| T Test, Welch Test 의 이해와 R 실습 (1) | 2017.09.25 |
| R을 활용한 변곡점 탐색하기 (loess function) :: Data 쿡북 (0) | 2017.08.20 |
| R을 활용한 요인 분석(인자분석, Factor Analysis) 정리 :: Data 쿡북 (5) | 2017.03.17 |
| R을 활용한 공분산과 상관계수 이해 :: Data 쿡북 (0) | 2017.03.12 |










댓글